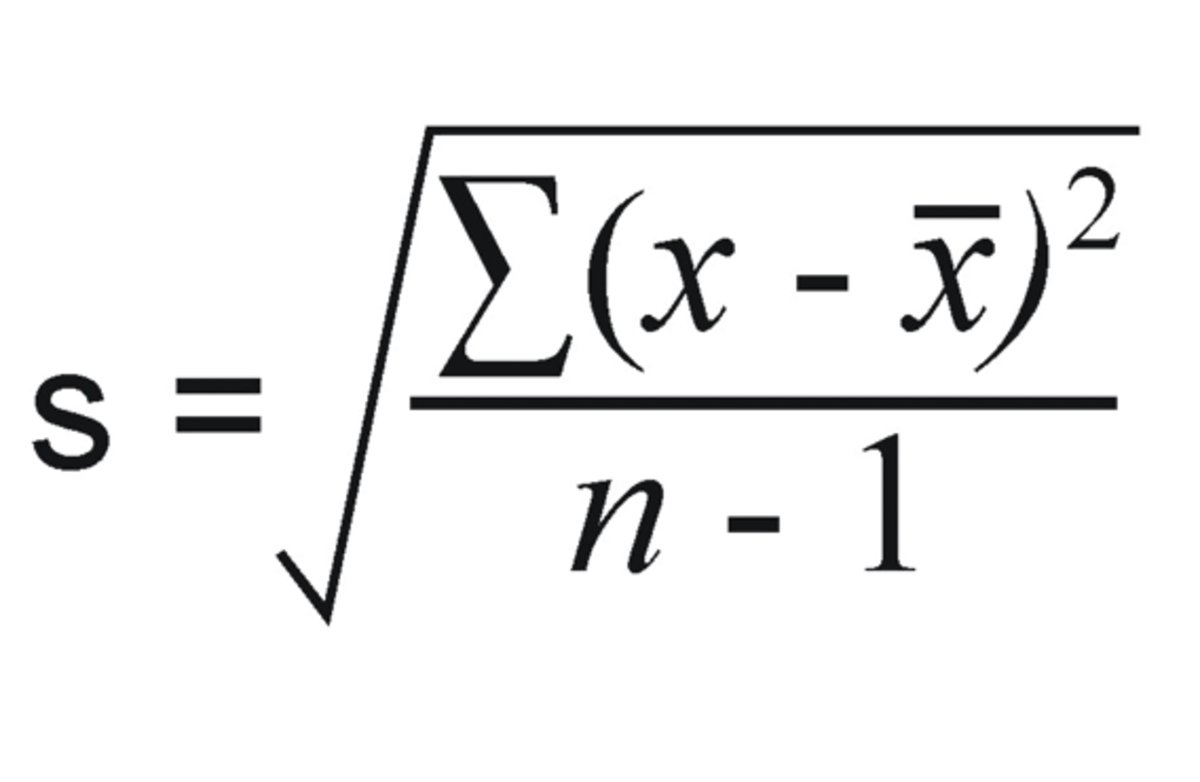Are you ready to dive into the world of statistics and sharpen your math skills? In this blog post, we will be exploring the concept of standard deviation and how to calculate it. Standard deviation is a crucial measure of variability or dispersion in a data set and is widely used in various fields such as science, finance, and engineering. We will start by understanding the concept of standard deviation and its significance in analyzing data. Next, we will discuss the process of gathering relevant data for calculations and understanding the importance of a well-organized data set. Then, we will delve into the step-by-step process of calculating the mean and finding the variance of the data set, followed by the application of the formula for standard deviation. So, grab a pen and paper, and let’s explore the fascinating world of standard deviation together!Learn how to calculate standard deviation step by step: understanding, gathering data, mean calculation, variance, and applying the formula for accurate results.
Understanding standard deviation
Standard deviation is a statistical measure of the amount of variation or dispersion of a set of values. It provides a way to understand how spread out the values in a data set are from the mean. In simpler terms, standard deviation tells us how much the numbers in a data set differ from the average of those numbers.
When calculating standard deviation, it’s important to first gather data for the calculations and then find the mean of the data set. Once the mean is calculated, we can proceed to find the variance of the data set, and finally apply the formula for standard deviation to obtain the result. Using the li tag for listing the steps and the table tag for displaying the numerical values can help with organizing the calculation process.
Gathering data for calculations
How to Calculate standard deviation
Before you can calculate standard deviation, you first need to gather the data that you will be using for the calculations. This can involve collecting measurements, observations, or any other type of data points that are relevant to the specific analysis you are conducting. The data you gather should be representative of the population or sample you are studying, and should be as complete and accurate as possible to ensure the accuracy of your calculations.
One way to organize the data you have gathered is to create a table that lists each data point. This can help you to easily see the range and distribution of the data, as well as determine if there are any outliers or anomalies that may need to be taken into account during the calculation process. By using a table to organize your data, you can ensure that you have all the information you need to proceed with the standard deviation calculation.
Calculating the mean of the data set
When it comes to data analysis, finding the mean of a data set is a crucial step in understanding the central tendency of the data. The mean, also known as the average, is calculated by summing up all the values in the data set and then dividing by the total number of values. This gives us a single value that represents the central point of the data distribution.
For example, if we have a data set of 10, 20, 30, 40, and 50, to find the mean, we would add all these values together (10 + 20 + 30 + 40 + 50 = 150) and then divide by the total number of values (in this case, 5). So, the mean of this data set would be 150/5 = 30. This means that on average, the values in the data set are around 30.
Finding the variance of the data set
When it comes to calculating the standard deviation of a data set, the first step is finding the variance. Variance measures how far each number in the set is from the mean and is crucial in understanding the spread of the data. To find the variance, start by calculating the mean of the data set. Once you have the mean, take each number in the data set and subtract the mean from it. Then, square the result of each of these differences. After squaring, find the mean of these squared differences. This mean is the variance of the data set.
Using the formula for variance, represented as σ^2 = Σ(x – μ)^2 / N, where σ^2 is the variance, Σ is the summation symbol, x is each individual number in the data set, μ is the mean, and N is the total number of data points. This formula calculates the average of the squared differences from the mean of the data set, providing a measure of how much the numbers deviate from the mean. Once the variance is found, it can be used to then calculate the standard deviation, another important measure of dispersion in the data set.
Applying the formula for standard deviation
Once you have gathered the data and calculated the mean and variance of the data set, the next step is to apply the formula for standard deviation. The standard deviation formula is a crucial part of statistical analysis, as it helps to quantify the amount of variation or dispersion of a set of values.
To calculate the standard deviation, you can use the following formula:
√variance = standard deviation.
Alternatively, you can also use the formula:
√(Σ(xi – x̄)² / N), where Σ represents the sum of all values, xi is each individual value, x̄ is the mean, and N is the total number of values in the data set.
| Data Set | Mean (x̄) | Variance | Standard Deviation |
|---|---|---|---|
| 10, 15, 20, 25, 30 | 20 | 50 | √50 = 7.07 |
Frequently Asked Questions
What is standard deviation?
Standard deviation is a measure of the amount of variation or dispersion of a set of values.
Why is standard deviation important?
Standard deviation is important because it gives an idea of how much individual values in a dataset differ from the mean.
How do you calculate standard deviation?
To calculate standard deviation, first find the mean of the values, then find the difference of each value from the mean, square those differences, find the mean of those squared differences, and finally take the square root of that mean.
What does a high standard deviation indicate?
A high standard deviation indicates that the values in the dataset are spread out over a wider range.
Can standard deviation be negative?
No, standard deviation cannot be negative as it represents a measure of dispersion and is always non-negative.
What does a standard deviation of zero mean?
A standard deviation of zero means that all the values in the dataset are the same.
What are some practical applications of standard deviation?
Standard deviation is commonly used in finance to measure investment risk, in scientific research to analyze data variability, and in quality control to monitor production processes.